Résoudre les équations logarithmiques
Résoudre des équations logarithmiques est quelque chose que vous devrez faire souvent lorsque vous traitez de procédures algébriques, et il vaut la peine de développer une stratégie concrète pour les traiter.
Ce que vous apprendrez dans ce didacticiel, ce sont les principales stratégies que vous devez suivre pour résoudre les équations logarithmiques.
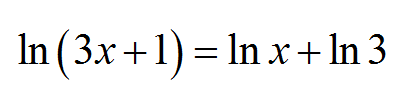
Quelle est l'équation logarithmique?
La première chose à laquelle nous devons définir une équation logarithmique.
Une équation logarithmique est une équation qui implique au moins une variable inconnue, où une expression logarithmique apparaît sur au moins un côté de l'équation
.
Un exemple d'équation logarithmique est
\[\ln x = 2\ln x - \ln 3\]ou aussi
\[ \ln(3x-1) - \ln(2x + 1) = 1\]
Notez qu'une équation logarithmique peut contenir plus d'un inconnu, comme par exemple
Stratégies de résolution des équations logarithmiques
La première responsabilité est que la résolution d'une équation logarithmique n'existe pas d'une équation logarithmique, ni d'une équation générale à ce sujet.La raison en est que toutes les méthodes supposent une certaine structure dans l'équation, ce qui n'est pas nécessairement là dans toutes les équations.
Donc, nous ne pouvons pas trouver la manière de résoudre des équations logarithmiques, car il n'ya aucune façon de traiter avec tous les cas possibles.
Pourtant, il y a quelques stratégies à suivre qui vous donneront la meilleure chance de passer par l'équation et de trouver une solution, si l'on existe.
Tout d'abord, essayez de regrouper toute expression logarithmique dans une expression logarithmique.
Ceci est obtenu typiquement en utilisant le plus courant Règles du Journal , cela vous permet de compacter une expression logarithmique si la structure de l'expression le permet.
Deuxièmement, une fois que les expressions logarithmiques sont compactées autant que possible, vous vous en débarrasserez en appliquant généralement la fonction exponentielle aux deux côtés de l'égalité.
Cette dernière étape, espérons-le, supprimera tous les logarithmes de l'image et vous permettra de résoudre pour l'inconnu (s).
Ainsi, en d'autres termes, la résolution d'une équation logarithmique consiste à regrouper les expressions logarithmiques, en les éliminant en appliquant exponentielle, puis résolvez l'équation comme une équation régulière.
Évidemment, lorsque vous vous êtes débarrassé des logarithmes, vous faites face à une équation qui pourrait avoir ses propres défis.
Résoudre des exemples différents d'équations logarithmiques
Il n'y a pas de meilleur moyen d'apprendre à résoudre des équations que de pratiquer réellement les résoudre:
EXEMPLE 1:
Résoudre l'équation suivante:
\[\large 4 \log(\sqrt x) = \log(6x-1)\]RÉPONSE:
Suivons les stratégies.L'idée est de compacter les expressions logarithmiques autant que possible.C'est un appel de jugement, car l'idée principale est de se débarrasser essentiellement des logarithmes.
Utilisation des règles du journal, nous pouvons mettre le "4" à l'intérieur du logarithme comme
\[\large 4 \log(\sqrt x) = \log(6x-1)\] \[\large \Rightarrow \log((\sqrt x)^4) = \log(6x-1)\] \[\large \Rightarrow \log(x^2) = \log(6x-1)\]Maintenant que les expressions logarithmiques sont aussi compactées que possible, nous devons nous débarrasser des logarithmes.
Une façon de le faire est d'appliquer la fonction exponentielle \(10^x\) à chaque côté de l'égalité.Qu'est-ce que je veux dire par là ???
Eh bien, vous avez deux côtés dans cette égalité.Étant donné que les deux côtés sont les mêmes, lorsqu'ils sont utilisés comme arguments de la fonction \(10^x\), il devrait préserver l'égalité.Nous avons donc
\[\large \log(x^2) = \log(6x-1)\] \[\large \Rightarrow 10^{\log(x^2)} = 10^{\log(6x-1)}\] \[\large \Rightarrow x^2 = 6x-1\]Parce que nous savons que \(10^{\log a} = a\), qui est l'une des règles de base du journal.
Alors maintenant que nous avons éliminé les logarithmes, nous pouvons résoudre l'équation qui reste:
\[\large x^2 = 6x-1\] \[\large \Rightarrow x^2 - 6x + 1 = 0\] \[\large \Rightarrow x = \frac{-(-6) \pm \sqrt{(-6)^2-4(1)(1)}}{2(1)}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{36-4}}{2}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{32}}{2}\] \[\large \Rightarrow x = \frac{6 \pm 4\sqrt{2}}{2}\] \[\large \Rightarrow x = 3 \pm 2\sqrt 2\]Alors alors \(x_1 = 3 + 2\sqrt 2\) et \(x_2 = 3 - 2\sqrt 2\).Techniquement, vous devez vérifier si ces deux sont des solutions de l'équation d'origine, afin de s'assurer qu'ils appartiennent au domaine des expressions logarithmiques.
Dans ce cas, \(x_1 = 3 + 2\sqrt 2\) et \(x_2 = 3 - 2\sqrt 2\) sont les solutions de l'équation d'origine.
Exemple 2:
Résolvez l'équation logarithmique suivante:
\[\large \ln 5 - \ln(6-x) = \ln x\]RÉPONSE:
Utilisation des règles du journal, nous pouvons compacter les expressions du journal, nous obtenons que
\[\large \ln 5 - \ln(6-x) = \ln x\] \[\large \displaystyle \Rightarrow \ln\left(\frac{5}{6-x}\right) = \ln x\] \[\large \displaystyle \Rightarrow e^{\ln\left(\frac{5}{6-x}\right)} = e^{\ln x}\] \[\large \displaystyle \Rightarrow \frac{5}{6-x} = x\]Parce que nous savons que \(e^{\ln a} = a\), qui est l'une des règles de base du journal.
Par conséquent, maintenant que nous avons éliminé les logarithmes, nous pouvons résoudre l'équation que nous avons laissée:
\[\large \displaystyle \frac{5}{6-x} = x\] \[\large \displaystyle \Rightarrow 5 = x(6-x)\] \[\large \displaystyle \Rightarrow 5 = 6x - x^2\] \[\large \displaystyle \Rightarrow x^2 -6x + 5 = 0\] \[\large \displaystyle \Rightarrow (x-1)(x-5) = 0\]Alors alors \(x_1 = 1\) et \(x_2 = 5\).Branlons ces valeurs dans l'équation initiale pour voir si elles sont en fait des solutions:
Pour \(x_1 = 1\):
qui est la même chose que:
\[\large \ln 5 - \ln(5) = 0\]Ce qui est vrai, alors l'équation tient.
Pour \(x_1 = 5\):
qui est la même chose que:
\[\large \ln 5 - \ln(1) = \ln(5)\]Ce qui est vrai, alors l'équation tient.
Par conséquent, les solutions à l'équation sont \(x_1 = 1\) et \(x_2 = 5\).
En savoir plus sur la résolution des équations logarithmiques
Une chose que les étudiants sont les plus préoccupés par le fait est de vous débarrasser de la connexion à une équation.Mais nous avons vu que c'est en fait la partie facile.Ce qui est plus difficile, c'est d'utiliser réellement l'expression de manière algébrique afin que les journaux puissent être supprimés.
Cela soulève la question de savoir comment traiter différentes bases, ce qui nécessite son propre paragraphe.
Résoudre des équations logarithmiques avec des bases différentes
Dans les exemples ci-dessus, nous n'avons traité que \(\log\) (logarithm avec base 10) et \(\ln\) (logarithme avec base \(e\)).Comment le faites-vous lorsque vous avez un logarithme avec une base différente, comme \(\log_a\) ???
La réponse est simple: afin d'éliminer les logarithmes avec une base différente, dites \(\log_a\) qui a une base \(a\) nous utilisons simplement la fonction exponentielle \(a^x\).Juste juste ??
En effet, éliminer le logarithme est la partie facile des équations de logving.La partie plus difficile du processus est de grouper et de compacter les expressions logarithmiques sous une forme que vous les éliminez.
Vous pouvez en apprendre davantage sur la façon dont la fonction logarithmique fonctionne en voyant LES PROPRIÉTÉS DE SON GRAPHIQUE et étudier la Règles de Base du Journal .